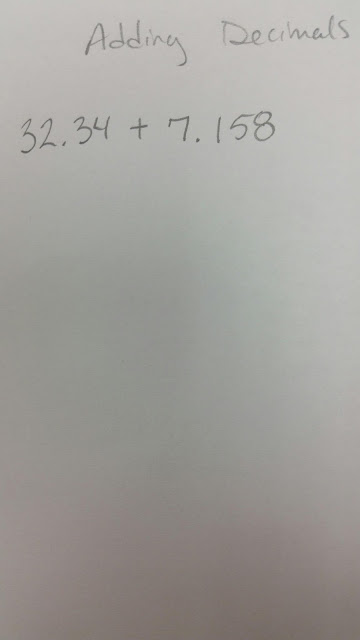Volume is how much space is inside an object. In our case, we use v=l x w x h to solve. See example below.
Mr. German's Math Class
Wednesday, February 28, 2018
Tuesday, February 27, 2018
Surface Area
The last section is over surface area. This can be hard because we have to imagine a 3d object and turn it in our minds. I am going to do my best to show you can example.
Below we have a rectangular prism with dimensions of 1 x 1 x 4. The order does not matter because we can flip this prism to fit what we need.
First, we are going draw a net on centimeter grid paper. We start by drawing the face we can see.
Then, we draw outside flaps, which are 1 x 1.
We finish by matching up the other dimensions. In this case, the rest will be 4 x 1. We match up the 2 dimensions from the bases (1 x 1) and match it to our 3rd dimension, 4.
Now that we have our net, we can count the boxes each part covers. OR, we can use the way shown below.
If you set all your dimensions out, 1 1 and 4, you can label them l w and h for length, width and height. Then you have to multiply each one by the other one. We have 3 numbers, so we will have 3 number sentences. The D stands for dimension, and the A stands for area of the face. LF means lateral faces, and lateral faces are congruent. Since a prism has 6 sides, we can multiply each number sentence by 2 to find the area of both lateral faces.
Always do the L X W, then L x H, then W x H. It doesn't matter when one you call which since we are multiplying. Then multiply each area by 2. As you can see in picture, the surface area of this net/prism, is 18 cm^2

Saturday, February 24, 2018
Finding Percents (Sales Tax)
The last section of this unit is dealing with finding percents. Since we are familiar with decimals and fractions (ratios included) we can use that knowledge to find percent. In order to find sales tax, we came up with a number sentence, or formula to help us out.
Total Cost = Price + Tax, where Tax = Tax Rate X Price.
We will abbreviate this to be
C = P + T, where T = % X P
Let's take a common item, like an Xbox One. The price for an Xbox One is $349. The tax is Conway (rounded up) is 9%. Since I cannot multiply by a %, I have to change that to a decimal. So we have to do that first. Since all percent is out of a hundred, we can write our percent as
9 = 0.09 as a decimal. Here is how to work the problem:
100
Total Cost = Price + Tax, where Tax = Tax Rate X Price.
We will abbreviate this to be
C = P + T, where T = % X P
Let's take a common item, like an Xbox One. The price for an Xbox One is $349. The tax is Conway (rounded up) is 9%. Since I cannot multiply by a %, I have to change that to a decimal. So we have to do that first. Since all percent is out of a hundred, we can write our percent as
9 = 0.09 as a decimal. Here is how to work the problem:
100
Alternatively, we can look at the cost of an item as having to pay
100% + 9% which would be 109%. This would be 1.09 as a decimal. So...
C = $349 X 1.09 = $380.41. Either way is fine.
But what if we know how much the tax was but forgot the price?
Let's say that our tax rate is 6% and we paid $4.80. We can use a percent bar and ratios to figure this out.
This percent bar shows what our 6% is, but not our 100%. We can use the ratios shown above. Since all percent is "out of 100" we can use 100 as a denominator and use what we know about equivalent ratios or fractions to get to 100%
We can also divide. We can use what we know fact families. Since
Tax = % (as a decimal) X price
Tax ÷ % (as a decimal) = price
$4.80 ÷ 0.06 = price
$80 = price
Friday, February 23, 2018
Percentages
Here is a chart to memorize for benchmark fractions, decimals, and percentages.
You can take any fraction and divide it to get a decimal. Let's look at 1/4.
Or you can take any decimal and turn it into a fraction by putting the place value as the denominator and whatever numbers are in your decimal as the numerator.
Or you can take any percentage and turn it into a fraction by placing it over 100 then change it to a decimal from there.
Lastly you can take the benchmarks and use them to your advantage. In the example, we used 25% which is equal to 1/4. From there we can get 50 and 75% plus we can do up to any number (we used 20 as a total) to find out each percentage of that number.
In summary, you can use these steps
If you have the part and the total, divide to get a decimal, the multiply by 100 to get the percent.
If you have the percent and the total, multiply to get the part.
Part ÷ Total = Percent
Percent x Total = Part
Tuesday, February 13, 2018
Area and Perimeter
The new unit is over Covering and Surrounding (area and perimeter). We used the formulas for area and perimeter or a rectangle to achieve this.
a = l x w p = 2 ( l + w )
We rearrange or use fact families to isolate (get a letter by itself) in order to solve for our missing letter.
As you can see, I have every variable by itself on one side of the equal sign. We do this by doing the opposite of what it tells use to do on the other side of the equal sign. Look at
a = l x w
If we do the opposite of multiply (x) which is divide, we can get
a ÷ l = w or a ÷ w = l
Perimeter is a little more complicated because we have two operations: multiply and add. Same rules apply though. The 2 outside the parentheses means to multiply, so we just divide that 2 on the other side of the equal sign.
p ÷ 2 = l + w.
Now we just subtract one of the other letters.
p ÷ 2 - w = l or p ÷ 2 - l = w
In class we used the second one, so for this example that is what we will use. It doesn't really matter though.
I like for the students to organize their problems by variables on the left side of their problem using
p =
l =
w =
This keeps everything organized. If we know a perimeter, we can substitute or replace the p with this number. Let's use 36 cm. Then we can guess at the length (l). For the example, I started with 2 cm because 36 cm is even and so is 2 cm. Look at the example. Notice my organization on the left and my formula at the top. Then follow the steps.
The only step I did here was to substitute what I know, or change p and l to 36 cm and 2 cm. Next I will complete the math.
I did the math in two steps and kept in mind order of operations. I completed 36 cm ÷ 2 and got 18 cm. Then I subtracted 18 cm - 2 cm to get 16 cm. This tells me that when my width is 2 cm, my length will be 16 cm for a rectangle with a perimeter of 36 cm.
In class, our job was to find ALL the possible lengths and widths for a given perimeter. We will do this again. This time, I will guess a length of 3 cm.
For a length of 3 cm and a perimeter of 36 cm, I will have a length of 15 cm. Notice my organization on the left and each step done separately on the right. Also notice that my equal signs are lined up. THIS IS MEGA IMPORTANT TO KEEP YOURSELF ORGANIZED. If we kept on doing this, we could complete a table. Here is the finished table.
Dimensions
|
Length
|
Width
|
Perimeter
|
Area
|
1 x 17
|
1
|
17
|
36
|
17
|
2 x 16
|
2
|
16
|
36
|
32
|
3 x 15
|
3
|
15
|
36
|
45
|
4 x 14
|
4
|
14
|
36
|
56
|
5 x 13
|
5
|
13
|
36
|
65
|
6 x 12
|
6
|
12
|
36
|
72
|
7 x 11
|
7
|
11
|
36
|
77
|
8 x 10
|
8
|
10
|
36
|
80
|
9 x 9
|
9
|
9
|
36
|
81
|
Once the length and the width are the same or close to the same, you have found all possibilities. You can then switch the lengths and the widths and have the same. (so instead of 1 x 17, you can have 17 x 1 and have the same perimeter and area).
Sunday, February 11, 2018
Tuesday, February 6, 2018
Area of a Triangle
We have moved onto area of a triangle. The concept remains the same: area means "what is covered" by an object. Since a triangle is a different object, we will have a different formula.
Any triangle is half of a larger rectangle.
The triangle is on the left. The dashed lines on the right triangle represent a hypothetical rectangle
The formula for AREA OF A RECTANGLE is a = l x w.
This can lead us to the area of a triangle by dividing the area of a rectangle by 2.
Below is another example worked out on the marker board. We used our knowledge of multiplying fractions.
Any triangle is half of a larger rectangle.
The triangle is on the left. The dashed lines on the right triangle represent a hypothetical rectangle
The formula for AREA OF A RECTANGLE is a = l x w.
This can lead us to the area of a triangle by dividing the area of a rectangle by 2.
a = l x w ÷ 2
With triangles, we don't call it length and width. We call it the base and the height, so we can change l and w to b and h.
a = b x h ÷ 2
The official formula for AREA OF A TRIANGLE is
a = 1/2 b x h
Here is a labeled triangle. The base and the height always create a right angle from perpendicular lines.
We are beginning to remove the x for multiply, so our formula would look like this
a = 1/2bh
Symbols touching or numbers touching symbols means to multiply.
Let's look at an example:
We will then use our formula:
a = ? a = 1/2 (5) (6) since parentheses means multiply ( 5 x 6 )
b = 5 in a = 1/2 (30) then 1/2 x 30
h = 6 in a = 15 in^2 the ^ means exponent, or to the power of
(read 15 inches squared or 15 square inches)Below is another example worked out on the marker board. We used our knowledge of multiplying fractions.
Click here for help with multiplying fractions.
One final note: the height isn't always inside the triangle. Sometimes you have to draw it outside. Also, any side can be a base as long at there is a perpendicular line drawn from base to the opposite vertex, or corner.
Subscribe to:
Posts (Atom)